\(\newcommand{L}[1]{\| #1 \|}\newcommand{VL}[1]{\L{ \vec{#1} }}\newcommand{R}[1]{\operatorname{Re}\,(#1)}\newcommand{I}[1]{\operatorname{Im}\, (#1)}\)

Rotation exercise

>>> #: standard imports
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> np.set_printoptions(precision=4)  # print arrays to 4 DP
>>> import nibabel as nib

>>> #: gray colormap and nearest neighbor interpolation by default
>>> plt.rcParams['image.cmap'] = 'gray'
>>> plt.rcParams['image.interpolation'] = 'nearest'

Preliminaries

Check the you have rotations.py in your current directory, or elsewhere on you Python path:

>>> #: Check import of rotations code
>>> from rotations import x_rotmat, y_rotmat, z_rotmat

Your task…

I have taken a copy of the first volume in ds107_sub012_t1r2.nii.

>>> #: the first volume of ds107_sub012_t1r2.nii
>>> img_4d = nib.load('ds107_sub012_t1r2.nii')
>>> data = img_4d.get_data()
>>> vol0 = data[..., 0]

Then I rotated it by:

• 0.1 radians around the x axis, then;
• 0.2 radians around the y axis, then;
• 0.3 radians around the z axis.

Here is that image for download rotated_volume.nii.

>>> #: the resulting rotated image
>>> rotated_img = nib.load('rotated_volume.nii')
>>> rotated_vol0 = rotated_img.get_data()
>>> rotated_vol0.shape
(64, 64, 35)

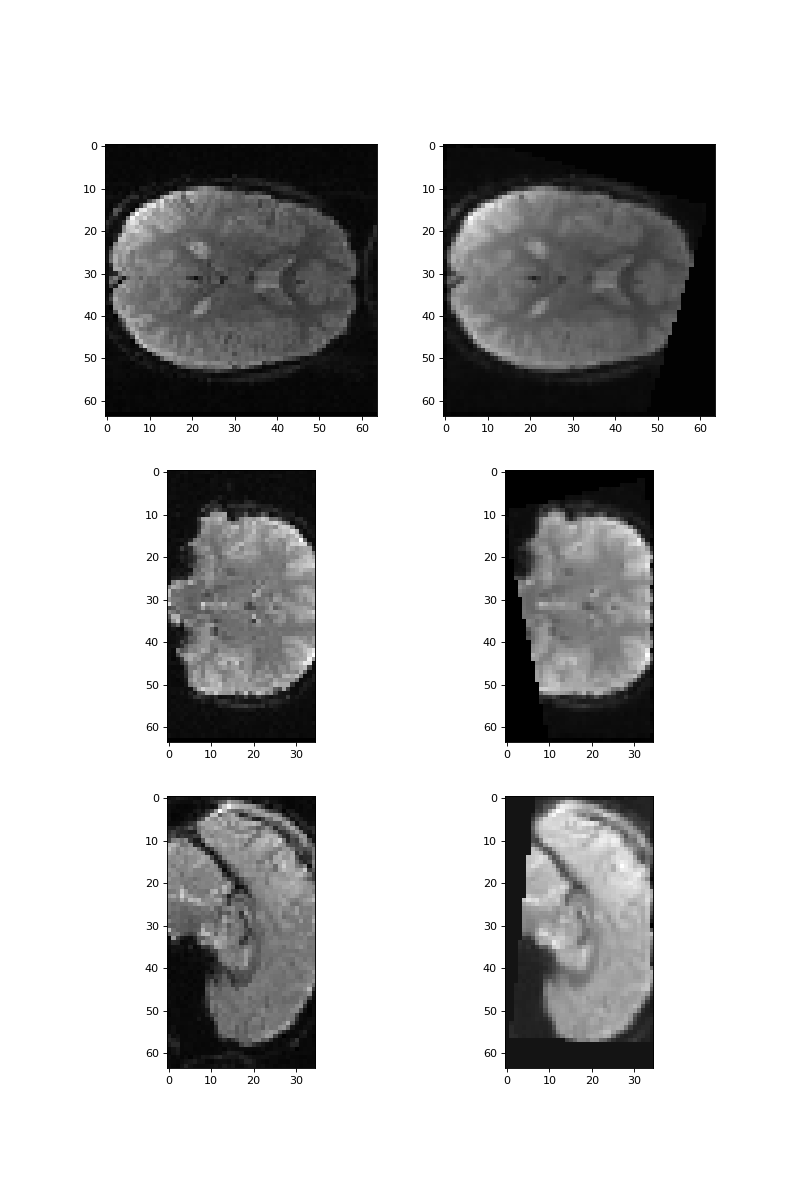
Here are slices over z, y, and x, for rotated and not-rotated images

>>> #: slices on z, y, and x axis for original and rotated images
>>> fig, axes = plt.subplots(3, 2, figsize=(10, 15))
>>> axes[0, 0].imshow(vol0[:, :, 17])
<...>
>>> axes[0, 1].imshow(rotated_vol0[:, :, 17])
<...>
>>> axes[1, 0].imshow(vol0[:, 31, :])
<...>
>>> axes[1, 1].imshow(rotated_vol0[:, 31, :])
<...>
>>> axes[2, 0].imshow(vol0[31, :, :])
<...>
>>> axes[2, 1].imshow(rotated_vol0[31, :, :])
<...>

(png, hires.png, pdf)

Of course, I have to be more specific by what I mean when I say that I rotated this image by:

• 0.1 radians around the x axis, then;
• 0.2 radians around the y axis, then;
• 0.3 radians around the z axis.

I am describing the mapping from coordinates in vol0 to coordinates in rotated_vol0.

As you now know, in order to apply this rotation, I needed to do pull resampling, so I needed to use the mapping from coordinates in rotated_vol0 to coordinates in vol0. So applying this rotation involved: rotation of -0.3 radians around z, then -0.2 radians around y then -0.1 radians around x.

Your task, should you chose to accept it, is to make a new image, where you have undone the given rotations.

Let’s remind ourselves of what we need to do.

In order to make the new fixed image, we will need to

1. Make a new empty image the same shape as the original;
2. For every coordinate \((i, j, k)\) in this new empty image, we are going to apply a transformation \(t\). This transformation will give us the corresponding coordinate \((i', j', k')\) in the rotated_vol0;
3. We use linear resampling to estimate a voxel value \(v\) for coordinate \((i', j', k')\) in rotated_vol0;
4. We put this voxel value \(v\) into the empty image at coordinate \((i, j, k)\).

In fact scipy.ndimage.affine_transform will do all these steps for us, but we need to supply the transformation \(t\).

So – what transformation do we need?

We are doing pull resampling - so we want the mapping from coordinates in vol0 to coordinates in rotated_vol0.

Your job is to make M – a 3 by 3 matrix that applies this mapping.

See rotation in 2d and Rotations and rotation matrices.

M is the matrix that scipy.ndimage.affine_transform will use to get the transformation between coordinates in the new empty image and the corresponding coordinates in the rotated image.

>>> #- Make a 3 by 3 transformation matrix that applies this sequence
>>> #- * 0.1 radians around the x axis, then
>>> #- * 0.2 radians around the y axis, then
>>> #- * 0.3 radians around the z axis.
>>> M = z_rotmat(0.3).dot(y_rotmat(0.2)).dot(x_rotmat(0.1))
>>> M
array([[ 0.9363, -0.2751,  0.2184],
       [ 0.2896,  0.9564, -0.037 ],
       [-0.1987,  0.0978,  0.9752]])

Use scipy.ndimage.affine_transform to create the new image and use the transform to sample from the rotated image:

>>> #- Use affine_transform to resample from `rotated_vol0` using the transform.
>>> #- Get the result into a variable `derotated_vol0`
>>> from scipy.ndimage import affine_transform
>>> derotated_vol0 = affine_transform(rotated_vol0, M)
>>> derotated_vol0.shape
(64, 64, 35)

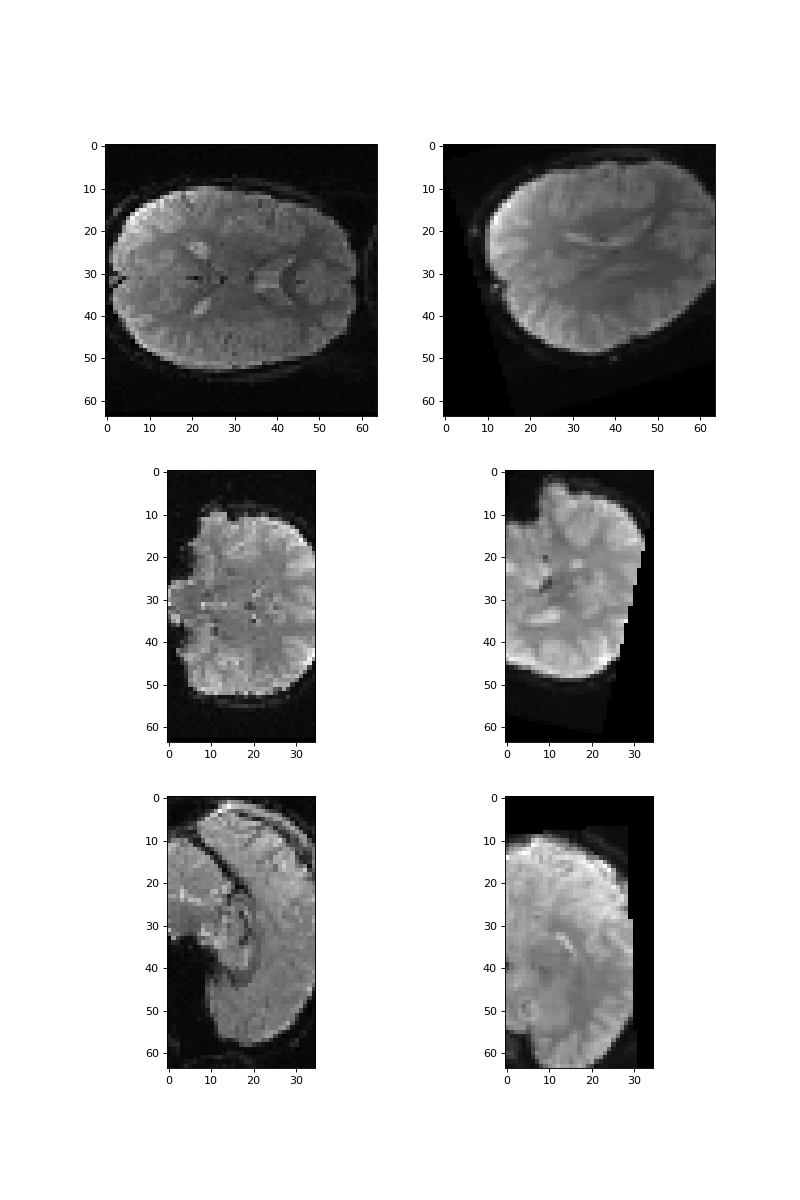
>>> #- plot slices from the image to see if you got the right transformation.
>>> fig, axes = plt.subplots(3, 2, figsize=(10, 15))
>>> axes[0, 0].imshow(vol0[:, :, 17])
<...>
>>> axes[0, 1].imshow(derotated_vol0[:, :, 17])
<...>
>>> axes[1, 0].imshow(vol0[:, 31, :])
<...>
>>> axes[1, 1].imshow(derotated_vol0[:, 31, :])
<...>
>>> axes[2, 0].imshow(vol0[31, :, :])
<...>
>>> axes[2, 1].imshow(derotated_vol0[31, :, :])
<...>

(png, hires.png, pdf)