\(\newcommand{L}[1]{\| #1 \|}\newcommand{VL}[1]{\L{ \vec{#1} }}\newcommand{R}[1]{\operatorname{Re}\,(#1)}\newcommand{I}[1]{\operatorname{Im}\, (#1)}\)
Optimizing rotation exercise¶
- For code template see:
optimizing_rotation_code.py; - For solution see: Optimizing rotation exercise.
>>> #: standard imports
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> np.set_printoptions(precision=4) # print arrays to 4 DP
>>> import nibabel as nib
>>> #: gray colormap and nearest neighbor interpolation by default
>>> plt.rcParams['image.cmap'] = 'gray'
>>> plt.rcParams['image.interpolation'] = 'nearest'
You will need rotations.py for this exercise:
>>> #: rotations module
>>> from rotations import x_rotmat, y_rotmat, z_rotmat
An affine normalization¶
In the last exercise – Rotation exercise – you undid a rotation.
In that case, I told you what the rotation was. What if I didn’t tell you? Could you work it out?
This is a good job for optimization.
>>> #: the first volume of ds107_sub012_t1r2.nii
>>> img_4d = nib.load('ds107_sub012_t1r2.nii')
>>> data = img_4d.get_data()
>>> vol0 = data[..., 0]
Here is the volume with some rotations I have applied:
secret_rotated_volume.nii. This time I’m not going to tell you
what rotations I applied:
>>> #: the secretly rotated image
>>> rotated_img = nib.load('secret_rotated_volume.nii')
>>> rotated_vol0 = rotated_img.get_data()
>>> rotated_vol0.shape
(64, 64, 35)
Displayed side by side with the original (not-rotated) image:
>>> #: slices on z, y, and x axis from
>>> fig, axes = plt.subplots(3, 2, figsize=(10, 15))
>>> axes[0, 0].imshow(vol0[:, :, 17])
<...>
>>> axes[0, 1].imshow(rotated_vol0[:, :, 17])
<...>
>>> axes[1, 0].imshow(vol0[:, 31, :])
<...>
>>> axes[1, 1].imshow(rotated_vol0[:, 31, :])
<...>
>>> axes[2, 0].imshow(vol0[31, :, :])
<...>
>>> axes[2, 1].imshow(rotated_vol0[31, :, :])
<...>
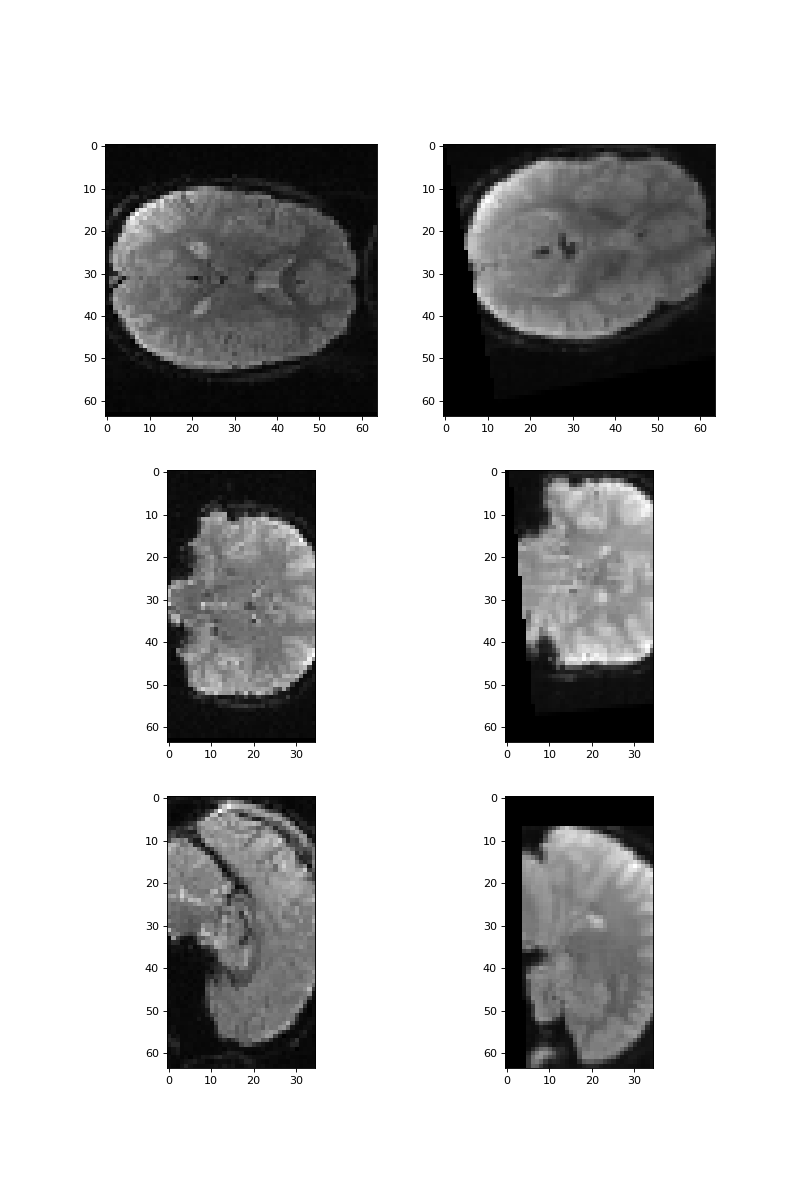
You might be able to work out what the transformations are, at least roughly, but can we work them out by optimization?
The first thing we need for optimization, is a mismatch metric.
I suggest you use the correlation mismatch function for the metric. You can get that from code in the optimizing space page, and paste it below. Feel free to try another mismatch metric if you like. Remember it is a function that accepts two images and returns a scalar that is low when the images are well matched.
>>> #- Get correlation mismatch metric from `optimizing_space`, paste here
Now we need a function that will transform a given image by a given set of rotations. The arguments will be:
vol_arr: the image that we will transform;rotations- a vector of rotations (one value for each of x, y, and z rotation).
The function then returns a copy of vol_arr with those rotations applied.
Specifically, the rotations give the resampling transform that gives the
mapping from coordinates in a new empty copy of vol_arr – call this
K – to coordinates in vol_arr.
Our vector of rotations is length 3, containing the \(r_x, r_y, r_z\), which are, respectively, the rotations about the x, y and z axis.
In order to do this transformation, you will need to take the three parameters, and convert them to the corresponding rotation matrix.
You then need to apply this transformation matrix to the coordinates of K
to return a new copy of vol_arr with \(r_x, r_y, r_z\) applied. Of
course, this will be a job for affine_transform:
>>> #: affine_transform function
>>> from scipy.ndimage import affine_transform
Your new function will look something like this:
def apply_rotations(vol_arr, rotations):
r_x, r_y, r_z = rotations
rotation_matrix = "what goes here?"
# apply rotations with affine_transform to make new image
# return new image
>>> #- Make apply_rotations function, accepting `vol_arr` and `rotations`
>>> #- vector, returning image with rotations applied.
>>> #: You could try this quick check that 0 rotations give the same
>>> # output back
>>> not_changed = apply_rotations(rotated_vol0, [0, 0, 0])
>>> assert np.allclose(not_changed, rotated_vol0)
Now we have the function to apply the rotations, and the matching function, we can make the cost function to optimize.
Use the global scope to pick up and use rotated_vol0 and vol0 in
the function.
>>> #- Make a cost function, that
>>> #- * is called 'cost_function'
>>> #- * accepts a vector of rotations as input
>>> #- * applies the vector of rotations to `rotated_vol0` from the global
>>> #- scope
>>> #- * returns the mismatch metric for the transformed copy of
>>> #- `rotated_vol0` and `vol0`
>>> #: a quick check the cost function returns the current value without rotations
>>> current = correl_mismatch(vol0, rotated_vol0)
>>> redone = cost_function([0, 0, 0])
>>> assert np.allclose(current, redone)
Now we are ready to optimize. We are going to need at least one of the cost functions from scipy.optimize.
fmin_powell is a good place to start:
>>> #: get fmin_powell
>>> from scipy.optimize import fmin_powell
Now call fmin_powell with some starting guess for the rotations:
>>> #- Call optimizing function and collect best estimates for rotations
Finally, use these parameters to:
- compile the rotation matrix from the optimized parameters. This gives the
matrix mapping from coordinates in
vol0to coordinates inrotated_vol0; - Use
affine_transformonrotated_vol0to get an un-rotated version of that image.
You should be able to do this with your apply_rotations function:
>>> #- Use 'apply_rotations' and the estimated parameters to un-rotate the
>>> #- rotated image
>>> #- Put the new un-rotated image into a variable `best_vol0`
Now you can look at the original and the un-rotated image side by side:
>>> #- slices on z, y, and x axis from original and un-rotated image
If you like, you can check in the file make_rotated.py to see what
rotation I actually applied.
If you raced ahead¶
Why not try another mismatch function?
And / or try another fmin_ function from scipy.optimize?
Is it easy for the optimization to go wrong, or is it nearly always right whatever parameter you choose?