\(\newcommand{L}[1]{\| #1 \|}\newcommand{VL}[1]{\L{ \vec{#1} }}\newcommand{R}[1]{\operatorname{Re}\,(#1)}\newcommand{I}[1]{\operatorname{Im}\, (#1)}\)

Anatomical solution

>>> #- Our usual imports
>>> import numpy as np  # the Python array package
>>> import matplotlib.pyplot as plt  # the Python plotting package

Now we will work with a 3D brain image.

Like the camera image in Cameraman solution, the pixel data for the 3D image is in a text file called anatomical.txt. Download anatomical.txt to your working directory.

I happen to know this image has length 32 on the third dimension, but I don’t know what the size of the first two dimensions are.

So, I know the image is of shape (I, J, 32), but I don’t know what I and J are.

Here are the first four lines of anatomical.txt.

0.0000
0.0000
53.0000
43.0000

The data is in the same floating point text format as the camera picture pixel data.

Read all the lines of the file into a list of float values, as before.

>>> #- Read file into list of float values
>>> pixel_values = []
>>> for line in open('anatomical.txt', 'r'):
...     pixel_values.append(float(line))

How many pixel values does this file contain?

>>> #- How many pixel values?
>>> len(pixel_values)
848640

When I have my image array correctly shaped, then, if I take a slice over the third dimension:

slice_on_third = image_array[:, :, 0]

slice_on_third will be shape (I, J) (the size of the first two dimensions).

How many pixel values does a slice in the third dimension contain - given that we know the third dimension is length 32? Put another way, what is the value for I * J?

>>> #- Find the size of a slice over the third dimension
>>> # P = ?
>>> P = len(pixel_values) / 32
>>> P
26520.0

Call P the number of values per slice on the third dimension (so P == I * J where we don’t yet know I or J).

Is this slice over the third dimension square (does I == J)?

We need to find the values for I and J.

Find candidates for I by using the modulus operator (%) to find a few numbers between 120 and 200 that divide exactly into the slice size P. Hint: the first value will be 120.

>>> #- Find candidates for I
>>> candidates = []
>>> for i in range(120, 201):
...     if P % i == 0:
...         candidates.append(i)
>>> candidates
[120, 130, 136, 156, 170, 195]

These numbers are candidates for I - the first number in the pair (I, J). We now need to find the corresponding J for each candidate for I.

Use the integer division operator (//) to get a list of pairs of numbers I and J such that I * J == P. Hint: the first pair of I, J is (120, 221).

>>> #- Find candidate pairs for I, J
>>> pairs = []
>>> for candidate in candidates:
...     pair = [candidate, P // candidate]
...     pairs.append(pair)
>>> pairs
[[120, 221.0], [130, 204.0], [136, 195.0], [156, 170.0], [170, 156.0], [195, 136.0]]

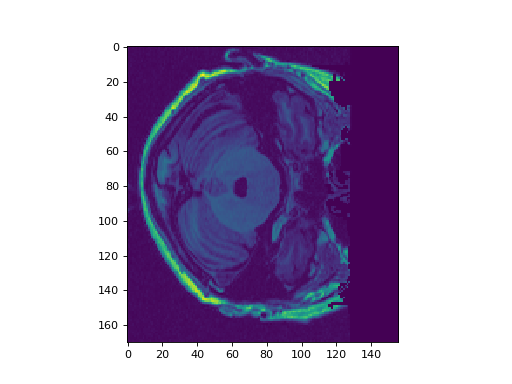
The full image shape will be three values, with one of these (I, J) pairs followed by 32. For example, the correct shape might be (120, 221 , 32) (it isn’t!). Try reshaping the pixel data with a few of the (I, J, 32) candidates to see which one is likely to be right. You might want to plot a slice over the third dimension to see how it looks.

>>> #- Try reshaping using some candidate pairs
>>> pixel_array = np.array(pixel_values)
>>> try1 = np.reshape(pixel_array, (130, 204, 32))
>>> plt.imshow(try1[:, :, 15])  # A middle slice in the third dimension
<...>

(png, hires.png, pdf)

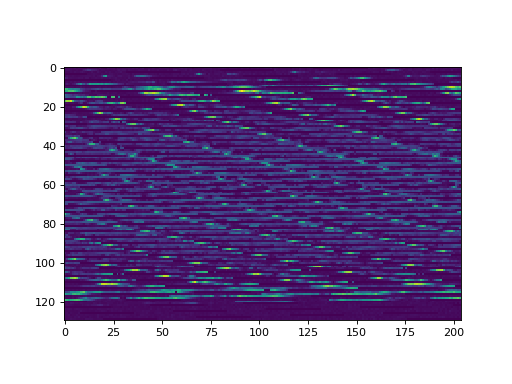
>>> try2 = np.reshape(pixel_array, (195, 136, 32))
>>> plt.imshow(try2[:, :, 15])  # Same slice
<...>

(png, hires.png, pdf)

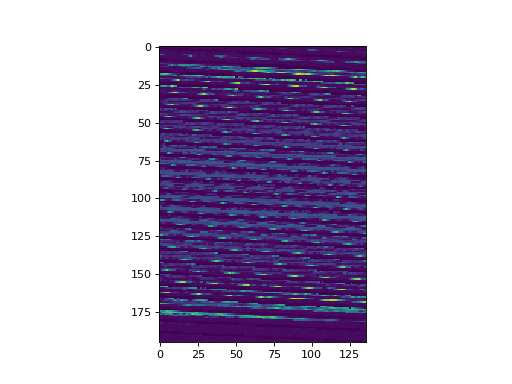
>>> try3 = np.reshape(pixel_array, (170, 156, 32))
>>> plt.imshow(try3[:, :, 15])
<...>

>>> # The last one looks good, so final shape is:
>>> try3.shape
(170, 156, 32)

(png, hires.png, pdf)