\(\newcommand{L}[1]{\| #1 \|}\newcommand{VL}[1]{\L{ \vec{#1} }}\newcommand{R}[1]{\operatorname{Re}\,(#1)}\newcommand{I}[1]{\operatorname{Im}\, (#1)}\)

General resampling between images with scipy.ndimage.map_coordinates

Requirements:

• coordinate systems and affine transforms;
• Making coordinate arrays with meshgrid;
• numpy.tranpose for swapping axes;
• The nibabel.affines module;
• Applying coordinate transforms with nibabel.affines.apply_affine;

scipy.ndimage.affine_transform is a routine that samples between images where there is an affine transform between the coordinates of the output image and the input image.

scipy.ndimage.map_coordinates is a more general way of resampling between images, where we specify the coordinates in the input image, for each voxel coordinate in the output image.

Instead of using the implied coordinate grid, we pass in an actual coordinate array.

This means that we can resample using coordinate transformations that cannot be expressed as an affine, such as complex non-linear transformations.

map_coordinates accepts:

• input – the array to resample from;
• coordinates – the array shape (3,) + output_shape giving the voxel coordinates at which to sample input;

Here the output_shape is implied by the shape of coordinates.

map_coordinates then makes an empty array shape K where K = coordinates.shape[1:]. For every index i, j, k implied by K.shape it:

• gets the 3-length vector coord = coordinates[:, i, j, k] giving the voxel coordinate in input;
• samples input at coordinates coord to give value v;
• inserts v into K with K[i, j, k] = v.

This might be clearer with an example. Let’s resample a structural brain image to a functional brain image. See Reslicing with affines exercise for an exercise using scipy.ndimage.affine_transform to do this.

You will need the:

• BOLD (functional) image : ds114_sub009_t2r1.nii;
• structural image : ds114_sub009_highres.nii.

>>> #: standard imports
>>> import numpy as np
>>> import numpy.linalg as npl
>>> # print arrays to 4 decimal places
>>> np.set_printoptions(precision=4, suppress=True)
>>> import matplotlib.pyplot as plt
>>> #: gray colormap and nearest neighbor interpolation by default
>>> plt.rcParams['image.cmap'] = 'gray'
>>> plt.rcParams['image.interpolation'] = 'nearest'
>>> import nibabel as nib

Load the structural and functional data:

>>> bold_img = nib.load('ds114_sub009_t2r1.nii')
>>> mean_bold_data = bold_img.get_data().mean(axis=-1)
>>> structural_img = nib.load('ds114_sub009_highres.nii')
>>> structural_data = structural_img.get_data()

We now now the transformation to go from voxels in the structural to voxels in the (mean) functional:

>>> mean_mm2vox = npl.inv(bold_img.affine)
>>> struct_vox2mean_vox = mean_mm2vox.dot(structural_img.affine)
>>> struct_vox2mean_vox
array([[ -0.2497,   0.0151,  -0.0027,  63.5174],
       [  0.0115,   0.3242,   0.0137,   1.1053],
       [ -0.0034,  -0.0176,   0.2496, -27.7359],
       [  0.    ,   0.    ,   0.    ,   1.    ]])

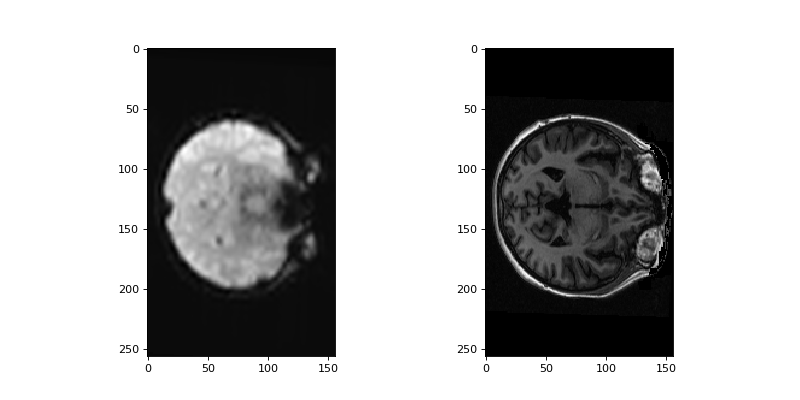
Sure enough, if we use this affine to resample the functional image, we get a functional image with the same voxel sizes and positions as the structural image:

>>> # Resample using affine_transform
>>> from scipy.ndimage import affine_transform
>>> mat, vec = nib.affines.to_matvec(struct_vox2mean_vox)
>>> resampled_mean = affine_transform(mean_bold_data, mat, vec,
...                                   output_shape=structural_data.shape)

>>> # Show resampled data
>>> fig, axes = plt.subplots(1, 2, figsize=(10, 5))
>>> axes[0].imshow(resampled_mean[:, :, 150])
<...>
>>> axes[1].imshow(structural_data[:, :, 150])
<...>

(png, hires.png, pdf)

We get the exact same effect with map_coordinates if we create the voxel coordinates ourselves, and apply the transform to them. We need numpy.meshgrid to make the initial coordinate array:

>>> # Get the I, J, K coordinates implied by the structural data array
>>> # shape
>>> I, J, K = structural_data.shape
>>> i_vals, j_vals, k_vals = np.meshgrid(range(I), range(J), range(K),
...                                      indexing='ij')
>>> in_vox_coords = np.array([i_vals, j_vals, k_vals])
>>> in_vox_coords.shape
(3, 256, 156, 256)

>>> in_vox_coords[:, 0, 0, 0]
array([0, 0, 0])

>>> in_vox_coords[:, 1, 0, 0]
array([1, 0, 0])

We transform the coordinate grid using nibabel’s apply_affine function:

>>> coords_last = in_vox_coords.transpose(1, 2, 3, 0)
>>> mean_vox_coords = nib.affines.apply_affine(struct_vox2mean_vox,
...                                            coords_last)
>>> coords_first_again = mean_vox_coords.transpose(3, 0, 1, 2)

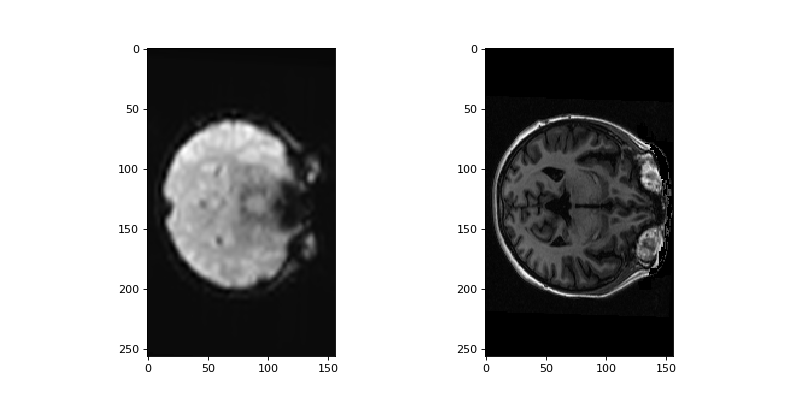
Use this with map_coordinates to get the same result as we got for affine_transform:

>>> # Resample using map_coordinates
>>> from scipy.ndimage import map_coordinates
>>> resampled_mean_again = map_coordinates(mean_bold_data,
...                                        coords_first_again)

>>> # Show resampled data
>>> fig, axes = plt.subplots(1, 2, figsize=(10, 5))
>>> axes[0].imshow(resampled_mean_again[:, :, 150])
<...>
>>> axes[1].imshow(structural_data[:, :, 150])
<...>

(png, hires.png, pdf)