\(\newcommand{L}[1]{\| #1 \|}\newcommand{VL}[1]{\L{ \vec{#1} }}\newcommand{R}[1]{\operatorname{Re}\,(#1)}\newcommand{I}[1]{\operatorname{Im}\, (#1)}\)

Affine optimization exercise

>>> #: standard imports
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> # print arrays to 4 decimal places
>>> np.set_printoptions(precision=4, suppress=True)
>>> import numpy.linalg as npl
>>> import nibabel as nib

>>> #: gray colormap and nearest neighbor interpolation by default
>>> plt.rcParams['image.cmap'] = 'gray'
>>> plt.rcParams['image.interpolation'] = 'nearest'

We need the rotations.py code:

>>> #: Check import of rotations code
>>> from rotations import x_rotmat, y_rotmat, z_rotmat

An affine normalization

In Optimizing rotation exercise we used optimization to find what rotations I had applied to a functional volume.

Now we’re going to have a shot at using optimization to do an affine spatial normalization.

First – the images. We will be using skull-stripped version of the structural image we have been using for the other exercises – ds114_sub009_highres_brain_222.nii.

The skull-stripped version comes from the OpenFMRI dataset, but the authors have used the FSL bet utility to do the skull stripping:

>>> #: ds114 subject 9 highres, skull stripped
>>> subject_img = nib.load('ds114_sub009_highres_brain_222.nii')
>>> subject_data = subject_img.get_data()
>>> subject_data.shape
(88, 78, 128)

An example slice, over the third dimension:

>>> #: an example slice of skull-stripped structural
>>> plt.imshow(subject_data[:, :, 80])
<...>

(png, hires.png, pdf)

The MNI template we want to match to is mni_icbm152_t1_tal_nlin_asym_09a_masked_222.nii:

>>> #: the MNI template - also skull stripped
>>> template_img = nib.load('mni_icbm152_t1_tal_nlin_asym_09a_masked_222.nii')
>>> template_data = template_img.get_data()
>>> template_data.shape
(99, 117, 95)

>>> #: example slice over the third dimension of the template
>>> plt.imshow(template_data[:, :, 42])
<...>

(png, hires.png, pdf)

We have a current mapping from the voxels in the template image to the voxels in the subject image, using the image affines. What is that mapping (template_vox2subject_vox)?

>>> #- Get affine mapping from template voxels to subject voxels
>>> template_vox2subject_vox = npl.inv(subject_img.affine).dot(template_img.affine)
>>> template_vox2subject_vox
array([[ -1.    ,   0.    ,   0.    ,  90.3506],
       [ -0.    ,   0.7691,   0.    , -18.22  ],
       [ -0.    ,  -0.    ,   1.    ,  50.6663],
       [  0.    ,   0.    ,   0.    ,   1.    ]])

Break up this affine into the 3 x 3 mat component and length 3 vec translation component. We’ll need to use those in affine_transform:

>>> #- Break up `template_vox2subject_vox` into 3x3 `mat` and
>>> #- length 3 `vec`
>>> mat, vec = nib.affines.to_matvec(template_vox2subject_vox)
>>> mat
array([[-1.    ,  0.    ,  0.    ],
       [-0.    ,  0.7691,  0.    ],
       [-0.    , -0.    ,  1.    ]])
>>> vec
array([ 90.3506, -18.22  ,  50.6663])

Use scipy.ndimage.affine_transform to make a new version of the subject image, resampled into the array size / shape of the template:

>>> #- Use affine_transform to make a copy of the subject image
>>> #- resampled into the array dimensions of the template image
>>> #- Call this resampled copy `subject_resampled`
>>> #- (we are going to use this array later).
>>> #- Use order=1 for the resampling (it is quicker)
>>> from scipy.ndimage import affine_transform
>>> subject_resampled = affine_transform(subject_data, mat, vec,
...                                      output_shape=template_data.shape,
...                                      order=1)

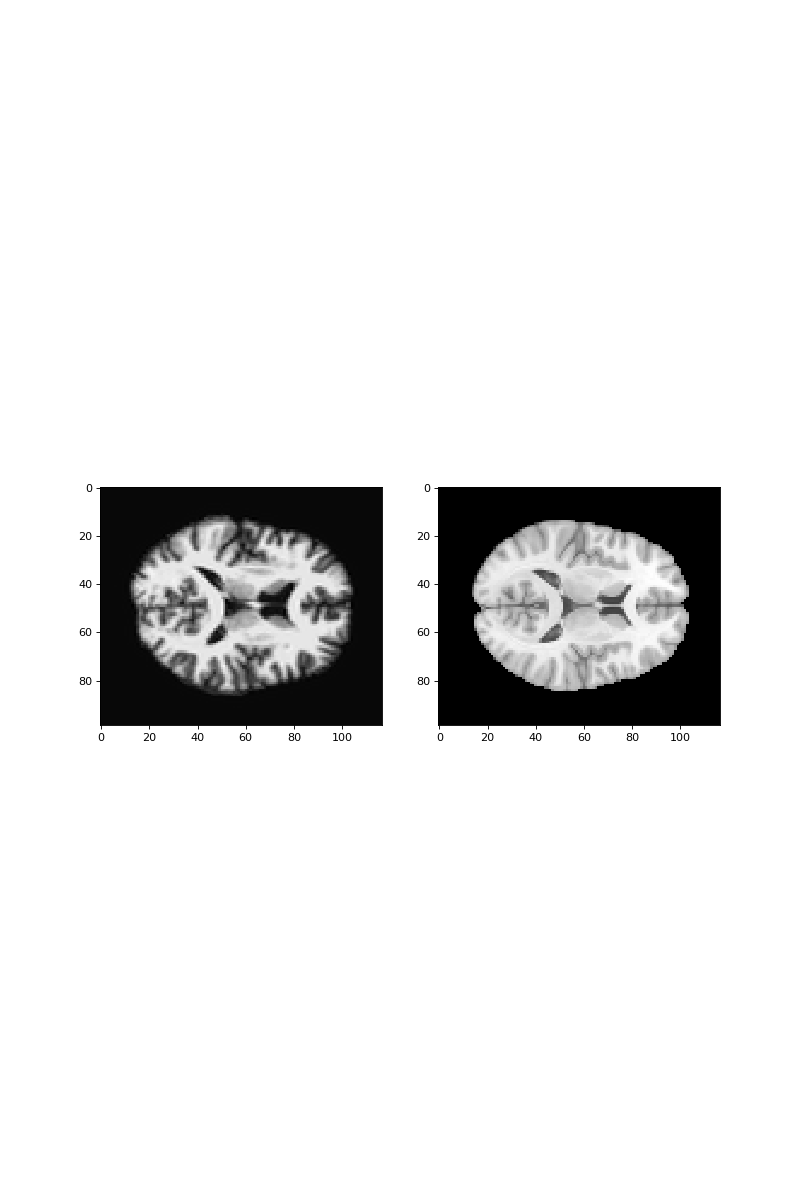
Plot a slice from the resampled subject data next to the matching slice from the template using subplots:

>>> #- Plot slice from resampled subject data next to slice
>>> #- from template data
>>> fig, axes = plt.subplots(1, 2, figsize=(10, 15))
>>> axes[0].imshow(subject_resampled[:, :, 42])
<...>
>>> axes[1].imshow(template_data[:, :, 42])
<...>

(png, hires.png, pdf)

Now we are going to try and do an affine match between these two images, using optimization.

We are going to need a cost function.

Remember, this takes the set of parameters we are using to transform the data, and returns a value that should be low when the images are well matched.

The value our cost function returns, is a mismatch metric.

I suggest you use the correlation mismatch function for the metric. Here is an implementation of the formula for the Pearson product-moment correlation coefficient:

\[r = r_{xy} =\frac{ \sum ^n _{i=1}(x_i - \bar{x})(y_i - \bar{y}) } { \sqrt{ \sum ^n _{i=1}(x_i - \bar{x})^2} \sqrt{\sum ^n _{i=1}(y_i - \bar{y})^2 } }\]

where \(\bar{x}\) is the mean:

\[\bar{x} = \frac{1}{n} \sum ^n _{i=1} x_i\]

The correlation makes sense here, because both the subject scan and the template are T1-weighted images, meaning that we expect gray matter to be gray, white matter to be white, and CSF to be black. So, when the images are well-matched, the signal in one image should correlate highly with the signal from matching voxels in the other.

>>> #: the negative correlation mismatch metric
>>> def correl_mismatch(x, y):
...     """ Negative correlation between the two images, flattened to 1D
...     """
...     x_mean0 = x.ravel() - x.mean()
...     y_mean0 = y.ravel() - y.mean()
...     corr_top = x_mean0.dot(y_mean0)
...     corr_bottom = (np.sqrt(x_mean0.dot(x_mean0)) *
...                    np.sqrt(y_mean0.dot(y_mean0)))
...     return -corr_top / corr_bottom

Let’s check this gives the same answer as the standard numpy function. Here we are using Random numbers with np.random to give us samples from the standard normal distribution:

>>> #: check numpy agrees with our negative correlation calculation
>>> x = np.random.normal(size=(100,))
>>> y = np.random.normal(size=(100,))
>>> assert np.allclose(correl_mismatch(x, y), -np.corrcoef(x, y)[0, 1])

Now we need a function that will transform the subject image, given a set of transformation parameters.

Let’s use these transformation parameters:

• x_t : translation in x;
• y_t : translation in y;
• z_t : translation in z;
• x_r : rotation around x axis;
• y_r : rotation around y axis;
• z_r : rotation around z axis;
• x_z : zoom (scaling) in x;
• y_z : zoom (scaling) in y;
• z_z : zoom (scaling) in z.

Say vol_arr is the image that we will transform.

Our function then returns a copy of vol_arr with those transformations applied.

Let’s also say that these transformations are in millimeters (x, y, z coordinates).

That means we are going to make these transformations into a new 4 x 4 affine P, and compose it with the template and subject affines:

• first - apply template_vox2mm mapping to map to millimeters;
• next - apply P affine made up of our transformations above;
• next - apply mm2subject_vox;
• call the result Q.

Finally, we want to apply the transformations in Q to make a resampled copy of the subject image.

Our first task is to take the 9 parameters above, and return the affine matrix P.

This function will look something like this:

def params2affine(params):
    # Unpack the parameter vector to individual parameters
    x_t, y_t, z_t, x_r, y_r, z_r, x_z, y_z, z_z = params
    # Matrix for zooms?
    # Matrix for rotations?
    # Vector for translations?
    # Build into affine

Hint: remember you have already imported x_rotmat etc from our rotations module.

>>> #- Make params2affine function
>>> #- * accepts params vector
>>> #- * builds matrix for zooms
>>> #- * builds atrix for rotations
>>> #- * builds vector for translations
>>> #- * compile into affine and return
>>> def params2affine(params):
...     # Unpack the parameter vector to individual parameters
...     x_t, y_t, z_t, x_r, y_r, z_r, x_z, y_z, z_z = params
...     # Matrix for zooms
...     zooms = np.diag([x_z, y_z, z_z])
...     # Matrix for rotations
...     x_rot = x_rotmat(x_r)
...     y_rot = y_rotmat(y_r)
...     z_rot = z_rotmat(z_r)
...     # Vector for translations
...     vec = [x_t, y_t, z_t]
...     # Build into affine
...     mat = x_rot.dot(y_rot).dot(z_rot).dot(zooms)
...     return nib.affines.from_matvec(mat, vec)

>>> #: some checks that the function does the right thing
>>> # Identity params gives identity affine
>>> assert np.allclose(params2affine([0, 0, 0, 0, 0, 0, 1, 1, 1]),
...                    np.eye(4))
>>> # Some zooms
>>> assert np.allclose(params2affine([0, 0, 0, 0, 0, 0, 2, 3, 4]),
...                    np.diag([2, 3, 4, 1]))
>>> # Some translations
>>> assert np.allclose(params2affine([0, 0, 0, 0, 0, 0, 2, 3, 4]),
...                    np.diag([2, 3, 4, 1]))
>>> # Some rotations
>>> assert np.allclose(params2affine([0, 0, 0, 0, 0, 0.2, 1, 1, 1]),
...                    [[np.cos(0.2), -np.sin(0.2), 0, 0],
...                     [np.sin(0.2), np.cos(0.2), 0, 0],
...                     [0, 0, 1, 0],
...                     [0, 0, 0, 1],
...                     ])
>>> assert np.allclose(params2affine([0, 0, 0, 0, 0, 0.2, 1, 1, 1]),
...                    [[np.cos(0.2), -np.sin(0.2), 0, 0],
...                     [np.sin(0.2), np.cos(0.2), 0, 0],
...                     [0, 0, 1, 0],
...                     [0, 0, 0, 1],
...                     ])
>>> assert np.allclose(params2affine([0, 0, 0, 0, -0.1, 0, 1, 1, 1]),
...                    [[np.cos(-0.1), 0, np.sin(-0.1), 0],
...                     [0, 1, 0, 0],
...                     [-np.sin(-0.1), 0, np.cos(-0.1), 0],
...                     [0, 0, 0, 1],
...                     ])
>>> assert np.allclose(params2affine([0, 0, 0, 0.3, 0, 0, 1, 1, 1]),
...                    [[1, 0, 0, 0],
...                     [0, np.cos(0.3), -np.sin(0.3), 0],
...                     [0, np.sin(0.3), np.cos(0.3), 0],
...                     [0, 0, 0, 1],
...                     ])
>>> # Translation
>>> assert np.allclose(params2affine([11, 12, 13, 0, 0, 0, 1, 1, 1]),
...                    [[1, 0, 0, 11],
...                     [0, 1, 0, 12],
...                     [0, 0, 1, 13],
...                     [0, 0, 0, 1]
...                     ])

Now we know how to make our affine P, we can make our cost function.

The cost function should accept the same vector of parameters as params2affine, then:

• generate P;
• compose template_vox2mm, then P then mm2subject_vox to give Q;
• resample the subject data using the matrix and vector from Q (use order=1 resampling - it is quicker);
• return the mismatch metric for the resampled image and template.

We can pick up the subject data and template data from the global namespace <global scope_>:

>>> #- Make a cost function called `cost_function` that will:
>>> #- * accept the vector of parameters containing x_t ... z_z
>>> #- * generate `P`;
>>> #- * compose template_vox2mm, then P then mm2subject_vox to give `Q`;
>>> #- * resample the subject data using the matrix and vector from `Q`.
>>> #-   Use `order=1` for the resampling - otherwise it will be slow.
>>> #- * return the mismatch metric for the resampled image and template.
>>> def cost_function(params):
...     P = params2affine(params)
...     Q = npl.inv(subject_img.affine).dot(P).dot(template_img.affine)
...     mat,  vec = nib.affines.to_matvec(Q)
...     resampled = affine_transform(subject_data, mat, vec,
...                                  output_shape=template_img.shape,
...                                  order=1)
...     return correl_mismatch(template_data, resampled)

>>> #: check the cost function returns the previous value if params
>>> # say to do no transformation
>>> current = correl_mismatch(subject_resampled, template_data)
>>> redone = cost_function([0, 0, 0, 0, 0, 0, 1, 1, 1])
>>> assert np.allclose(current, redone)

Now we are ready to optimize. We are going to need at least one of the cost functions from scipy.optimize.

fmin_powell is a good place to start:

>>> #- get fmin_powell
>>> from scipy.optimize import fmin_powell

Let’s define a callback so we can see what fmin_powell is doing:

>>> #: a callback we will pass to the fmin_powell function
>>> def my_callback(params):
...    print("Trying parameters " + str(params))

Now call fmin_powell with a starting guess for the parameters. Remember to pass the callback with callback=my_callback.

This is going to take a crazy long time, dependingn on your computer. Maybe 10 minutes.

>>> #- Call optimizing function and collect best estimates for rotations
>>> #- Collect best estimates in `best_params` variable
>>> best_params = fmin_powell(cost_function, [0, 0, 0, 0, 0, 0, 1, 1, 1],
...                           callback=my_callback)
Trying parameters [...]
Optimization terminated successfully.
         Current function value: -0.92...
         Iterations: ...
         Function evaluations: ...
>>> best_params  # doctest: +SKIP
array([ -2.0349,  38.6679, -18.986 ,   0.0287,  -0.0075,   0.028 ,
         0.9215,   0.9484,   0.8877])

Finally, use these parameters to:

• compile the P affine from the optimized parameters;
• compile the Q affine from the image affines and P;
• resample the subject image using the matrix and vector from this Q affine.

>>> #- * compile the P affine from the optimized parameters;
>>> #- * compile the Q affine from the image affines and P;
>>> #- * resample the subject image using the matrix and vector from the Q
>>> #-   affine.
>>> P = params2affine(best_params)
>>> Q = npl.inv(subject_img.affine).dot(P).dot(template_img.affine)
>>> mat, vec = nib.affines.to_matvec(Q)
>>> best_subject_data = affine_transform(subject_data, mat, vec,
...                                      output_shape=template_img.shape)

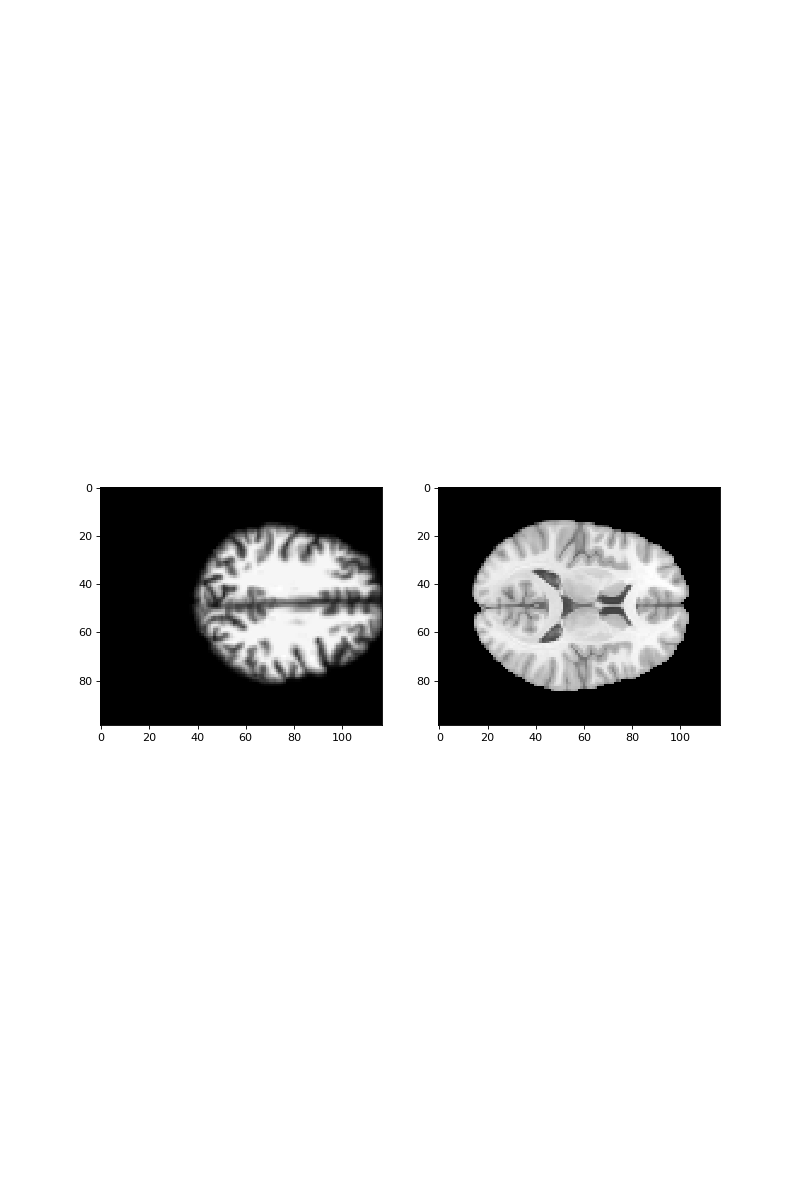
Now you can look at the template and the resampled affine-normalized image side by side, using Subplots and axes in matplotlib:

>>> #- show example slice from template and normalized image
>>> fig, axes = plt.subplots(1, 2, figsize=(10, 15))
>>> axes[0].imshow(best_subject_data[:, :, 42])
<...>
>>> axes[1].imshow(template_data[:, :, 42])
<...>

(png, hires.png, pdf)